Histogramm

Die erste Phase ist die Datenerhebung während der Herstellung. Diese Erfassung kann entweder ausnahmsweise während der Untersuchung der Variablen oder durch Verwendung einer automatischen oder manuellen Ablesung erfolgen, die während einer Kontrolle im Rahmen der Überwachung des Herstellungsprozesses durchgeführt wird.

Ohne dass es wirklich möglich ist, eine Mindestanzahl anzugeben, ist es erforderlich, dass die Anzahl der erfassten Werte ausreichend ist. Je größer die Anzahl der verfügbaren Werte, desto einfacher wird die Interpretation.

Die Wahl der Klassen, dh deren Anzahl und Breite, ist nicht eindeutig. Um sie zu bestimmen, ist es ratsam, sowohl die Art der Verteilung als auch die Anzahl der Datenpunkte zu berücksichtigen. Häufig werden bei einer derartigen Analyse Klassen gleicher Breite verwendet.

In der Literatur finden wir viele Vorschläge zur Auswahl der Klassenanzahl. Lassen Sie uns zum Beispiel zitieren:

• Die von Herbert Sturges (1926), der für N ungefähr normalverteilte Datenpunkte eine Anzahl von Klassen K vorschlägt, die mit der folgenden Formel erhalten werden:

K=1+Log2⁡NICHT≈1+103Log10⁡NICHT{\ displaystyle K = 1 + \ log _ {2} N \ approx 1 + {\ frac {10} {3}} \ log _ {10} N}

Zu diesem Thema kann man nützlicherweise den Artikel Rule of Sturges konsultieren .

• Die Alternative zur vorherigen Regel ist die sogenannte Regelregel, wobei

K=2⋅NICHT13{\ displaystyle K = 2 \ cdot N ^ {\ frac {1} {3}}}

• Die einfache Wahl der Quadratwurzel:

K=NICHT{\ displaystyle K = {\ sqrt {N}}}

Da das Histogramm ein visuelles Werkzeug ist, ist es auf jeden Fall möglich, die Anzahl der Klassen zu variieren. Dies ermöglicht es, das Histogramm mit einer unterschiedlichen Anzahl von Klassen zu sehen und so den besten Kompromiss zu finden, der die Interpretation erleichtert. Die Verwendung einer dedizierten Software oder einfacher einer Tabellenkalkulation erleichtert diesen Vorgang.

Die (minimale) Amplitude w des Histogramms ist

w=Maximalwert-Mindestwert{\ displaystyle w = {\ hbox {maximaler Wert}} - {\ hbox {minimaler Wert}} \,}

Um ein aussagekräftigeres Histogramm zu erhalten, kann es jedoch vorteilhaft sein, eine Amplitude zu wählen, die größer als die minimale Amplitude ist.

Die theoretische Amplitude h jeder Klasse ist dann:

ha=wK{\ displaystyle h = {\ frac {w} {K}}}

Dieser Wert sollte auf ein Vielfaches der Auflösung des Messgerätes gerundet (aufgerundet) werden.

Beispiel: Entweder die Masse einer kulinarischen Zubereitung vor dem Verpacken. Die Berechnung der Klassenamplitude ergibt h th = 0,014 kg . Die Auflösung der verwendeten Waage beträgt 0,001  kg . Der h-Wert wird auf 0,015 kg gerundet  .

Klassen können vom Typ [ untere Grenze  ; obere Grenze [oder] untere Grenze  ; obere Grenze ].

Der Mindestwert der ersten Klasse ergibt sich aus dem Mindestwert der Reihe minus einer halben Auflösung.

Beispiel: Der kleinste bei der Herstellung der Lebensmittelzubereitung erfasste Wert beträgt 0,498  kg . Die untere Grenze ist: 0,498 - (0,001 / 2) = 0,497 5  kg .

Der Einfachheit halber ist es vorzuziehen, einen "runden" Wert zu nehmen, zum Beispiel 0,495  kg

• Ein vollständig entwickeltes Beispiel finden Sie im Artikel: Kontinuierliche Elementarstatistik

Es gibt mehrere Möglichkeiten, die Höhe der Rechtecke zu bestimmen.

1. Die Höhen entsprechen den absoluten Häufigkeiten , dh für jedes Rechteck die Anzahl der Beobachtungen in der entsprechenden Klasse.
2. Die Höhen entsprechen den relativen Häufigkeiten , dh für jedes Rechteck der Anteil, beispielsweise in Prozent, der Beobachtungen in der entsprechenden Klasse.
3. Die Höhen werden so bestimmt, dass die Fläche des Rechtecks ​​der relativen Häufigkeit der Beobachtungen in der entsprechenden Klasse entspricht.

Das dritte Verfahren macht es auch möglich, Klassen mit variabler Breite unterzubringen, was nützlich ist, wenn die Daten in bestimmten Regionen, wie zum Beispiel in den Ausläufern der Verteilung, spärlich sind.

Entweder bei der Herstellung von Lebensmittelrationen, das Wiegen der Rationen vor dem Verpacken ergibt folgende Messreihen in kg:

Die Merkmale der Aussage sind wie folgt:

• Die Anzahl der Proben: N = 64
• Das Ausmaß: w = 0,098  kg
• Mindestwert: 0,498  kg
• Maximalwert: 0,596  kg

Wir leiten die folgenden Parameter für das Histogramm ab:

• Die Anzahl der Klassen beträgt 7 (unter Verwendung der Formel mit dem Logarithmus)
• Die Klassenamplitude beträgt 0,098 / 7 = 0,014  kg, die auf 0,015 kg aufgerundet wird  (Waagenauflösung: 0,001  kg )
• Der Mindestwert der ersten Klasse beträgt 0,498 - (0,001 / 2) = 0,4975. Zur leichteren Interpretation kann dieser Wert auf 0,495 kg gerundet werden  .

Wir erhalten das folgende Histogramm:

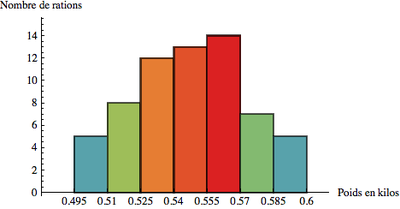
Interpretation

Die Verteilung vieler Industrieparameter entspricht oft einer Normalverteilung . Das erhaltene Histogramm wird oft mit dem "Glocken"-Profil der Normalverteilung verglichen. Dieser Vergleich ist visuell und auch wenn es ein erster Ansatz sein kann, stellt er keinen Test der „Normalität“ dar. Um dies zu tun, müssen Sie einen Test durchführen, von denen einer der klassischsten Henrys Linie ist .

Die Verteilung nach dem Normalgesetz ist, wenn sie extrem häufig ist, nicht systematisch. Wir prüfen, ob die Verteilung keiner Formfehlerverteilung entspricht (Beispiel: Messung der Exzentrizität in einem Rohr, Position von Gegenständen, die in Richtung einer Wand geschleudert werden, die teilweise von dieser Wand abprallen).

Die Interpretation kann beispielsweise folgende Ergebnisse liefern:

Im Fall eines Histogramms, das eine Mischung aus zwei Chargen mit unterschiedlichem Durchschnitt zeigt, gibt es Fälle, in denen die Dispersion diesen Aspekt aufweist, ohne jedoch eine Mischung zu belasten. Dies ist beispielsweise bei der Messung eines zylindrischen Teils der Fall , das jedoch einen Fehler vom ovalen Typ aufweist. Die beiden Mittelwerte repräsentieren dann den großen Durchmesser und den kleinen Durchmesser. Es ist die Kenntnis des Prozesses und / oder des Produkts, die diese Art der Interpretation ermöglicht.

Ein Werkzeug zum Schätzen einer Dichte

In diesem Abschnitt wird das Histogramm nicht als Visualisierungswerkzeug verwendet, sondern als statistische Schätzung der zugrunde liegenden Verteilung der Stichprobe. Wir haben eine Probe unabhängig und identisch nach einem Gesetz verteilt. Wir wollen aus der Stichprobe eine Schätzung der unbekannten Dichte ableiten, notiert f . x1,x2,⋯,xnicht{\ displaystyle x_ {1}, x_ {2}, \ cdots, x_ {n}}

Der diskrete Koffer

Wir suchen nach Wahrscheinlichkeiten , die die Verteilung charakterisieren. Wir bezeichnen diese Verteilung f mit Missbrauch. Ein natürlicher Schätzer ist: pich{\ displaystyle p_ {i}}

f^(x)=nicht(x)nicht{\ displaystyle {\ widehat {f}} (x) = {\ frac {n (x)} {n}}}

wobei die Anzahl der Beobachtungen in der Stichprobe ist, die gleich x sind . Eine alternative Möglichkeit, diesen Schätzer zu notieren, ist: nicht(x){\ Anzeigestil n (x)}

f^(x)=1nichtΣichnichtich(xich=x){\ displaystyle {\ widehat {f}} (x) = {\ frac {1} {n}} \ sum _ {i} ^ {n} I (x_ {i} = x)}

Wo ist die Indikatorfunktion: Sie ist 1 wert, wenn ihr Argument wahr ist. ich(⋅){\ displaystyle I (\ cdot)}

Der kontinuierliche Fall

Der bisherige Schätzer ist nicht mehr gültig, da wir im kontinuierlichen Fall die Anzahl der Beobachtungen nicht mehr genau gleich x zählen können . Auf der anderen Seite können wir eine Box mit der Mitte in x und der Breite h als positiven Parameter betrachten. Wir können die Anzahl der Beobachtungen ungefähr (und nicht mehr genau ) gleich x zählen , indem wir die Beobachtungen zählen, die in diese Box fallen. Der Schätzer wird:

f^(x)=1nichthaΣichnichtich(-12≤xich-xha≤12){\ displaystyle {\ widehat {f}} (x) = {\ frac {1} {nh}} \ sum _ {i} ^ {n} I \ left (- {\ frac {1} {2}} \ leq {\ frac {x_ {i} -x} {h}} \ leq {\ frac {1} {2}} \ right)}

oder nochmal, indem du fragst  : jaich=(xich-x)/ha{\ displaystyle y_ {i} = (x_ {i} -x) / h}

f^(x)=1nichthaΣichnichtich(|jaich|≤12){\ displaystyle {\ widehat {f}} (x) = {\ frac {1} {nh}} \ sum _ {i} ^ {n} I \ left (| y_ {i} | \ leq {\ frac { 1} {2}} \ rechts)}

Der Parameter h steuert den Grad der Glätte der Schätzung und sollte mit Sorgfalt gesucht werden. Der bisherige Schätzer hat gute Eigenschaften, die mit denen einer kontinuierlichen Dichte vergleichbar sind:

• es ist positiv;
• es ist in das Gerät integriert.

Es hat jedoch einen großen Mangel, eine Dichte abschätzen zu können: Sie ist nicht kontinuierlich. Um Kontinuität zu erhalten, verwenden wir den Parzen- (oder Kernel-) Schätzer . Das Prinzip ist einfach: Es genügt, die Indikatorfunktion durch eine reelle Funktion zu ersetzen, die ein Gewicht zuweist, das umso wichtiger ist, als die Beobachtungen in der Nähe von x liegen . Als Beispiel hier zwei Dichteschätzungen nach der Kernel-Methode mit unterschiedlichen Parametern:

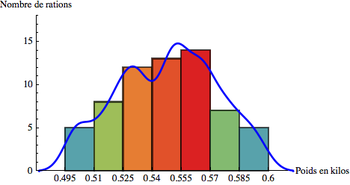
Ursprung

William Playfair ( Commercial and Political Atlas , 1786) ist der erste Förderer der Auswertung statistischer Beobachtungen durch Verteilungskurven und Balkendiagramme. Das Worthistogramm wurde 1895 von Pearson vorgeschlagen .

Hinweise und Referenzen

1. (in) Herbert Sturges, „  Die Wahl eines Klassenintervalls  “ , J. Amer. Statistiker. Assoc. , N o  21,1926, s.  65-66
2. Maurice Pillet, Anwendung der statistischen Kontrolle von MSP/SPC-Prozessen , Les ditions d'Organisation, 1995
3. Online-Statistikausbildung: Ein Multimedia-Studiengang ( http://onlinestatbook.com/ ). Projektleiter: David M. Lane, Rice University (Kapitel 2 "Grafische Verteilungen", Abschnitt "Histogramme")
4. Fix, E., Hodges Jr., J., 1951. Diskriminierende Analyse: Nichtparametrische Diskriminierung: Konsistenzeigenschaften. Bericht Nr. 4, USAF School of Aviation Medicine, Randolph Field, TX.

Siehe auch

Literaturverzeichnis

• Maurice Lethielleux, Descriptive Statistics , Dunod-Ausgaben, Paris, 1999 ( ISBN  2 10 003513 4 ) , 124 Seiten.
• Maurice Pillet, Anwenden statistischer Kontrolle von MSP/SPC-Prozessen , Les ditions d'Organisation, 1995 ( ISBN  2-7081-1774-2 ) , 336 Seiten.
• Pierre Souvay, Statistik und Qualität , AFNOR , Paris, Sammlung „Kennen“, 1994, 40 Seiten.
• Pierre Souvay, Wissen, wie man Statistiken verwendet, ein Werkzeug zur Entscheidungsfindung und Qualitätsverbesserung , AFNOR , Saint-Denis-la-Plaine , 2002 ( ISBN  2-12-475821-7 ) , 434 Seiten

Zum Thema passende Artikel

• Grafische Darstellungen statistischer Daten
• Perzentil
• Dezil
• Quantil
• Quartil

Externer Link

• Eine Methode zur Auswahl der Behältergröße eines Histogramms
• Kurs mit Beispielen für unterschiedliche Breitenklassen