Binomialstapel
In der Informatik ist ein Binomial Heap ist eine Datenstruktur , ganz ähnlich wie bei einem binären Heap , aber ermöglicht auch zwei Haufen schnell zusammengeführt werden. Daher unterstützt es die folgenden Operationen, alle in O (log n) :
- Fügen Sie ein neues Element in den Heap ein
- Suchen Sie den Artikel mit dem kleinsten Schlüssel
- Löschen Sie das Element mit dem kleinsten Schlüssel aus dem Heap
- Verringern Sie den Schlüssel eines bestimmten Elements
- Löschen Sie ein bestimmtes Element aus dem Heap
- Füge zwei Haufen zu einem zusammen
Der Binomialheap ist daher eine Implementierung des abstrakten zusammenführbaren Heap- Typs , dh eine Prioritätswarteschlange, die Zusammenführungsoperationen ermöglicht.
Binomialbaumkonzept
Ein Binomialheap ist in der Tat eine Menge von Binomialbäumen (zu vergleichen mit einem Binärheap, der einem einzelnen Binärbaum entspricht ). Ein Binomialbaum wird rekursiv wie folgt definiert:
- Der Binomialbaum der Ordnung 0 ist ein einfacher Knoten
- Der Binomialbaum der Ordnung k hat eine Wurzel vom Grad k und seine Kinder sind Wurzeln von Binomialbäumen der Ordnung k -1, k -2,…, 2, 1, 0 (in dieser Reihenfolge).
Ein Binomialbaum der Ordnung k kann auch aus zwei Bäumen der Ordnung k-1 konstruiert werden, indem einer der beiden zum Kind ganz links von der Wurzel des anderen gemacht wird. Ein Binomialbaum der Ordnung k hat 2 k Knoten und die Höhe k .
Varianten von Binomialbäumen werden auch verwendet, um Fibonacci-Haufen zu konstruieren .
Binomial-Heap-Struktur
Ein Binomialheap wird als eine Reihe von Binomialbäumen implementiert, die die Eigenschaften von Binomialheaps erfüllen :
- Jeder Binomialbaum im Heap hat eine geordnete Heap- Struktur : Der Schlüssel jedes Knotens ist größer oder gleich dem seines übergeordneten Knotens.
- Für jede natürliche ganze Zahl j existiert höchstens ein Binomialhaufen der Ordnung j .
Die erste Eigenschaft gibt an, dass die Wurzel jedes Binomialbaums den kleinsten Schlüssel im Baum hat. Die zweite Eigenschaft impliziert, dass ein Binomialheap, der n Elemente enthält, aus höchstens ln n + 1 Binomialbäumen besteht. Tatsächlich wird die Anzahl und die Reihenfolge dieser Bäume eindeutig durch die Anzahl n der Elemente bestimmt: Jedes Heap-Binomial entspricht Bit 1 in der binären Schrift der Zahl n . Zum Beispiel entspricht 13 1101 in Binärform, und daher besteht der Binomialheap mit 13 Elementen aus 3 Binomialbäumen der jeweiligen Ordnungen 3, 2 und 0 (siehe Abbildung unten). Die Wurzeln von Binomialbäumen werden in einer nach Baum indizierten Liste gespeichert Auftrag.
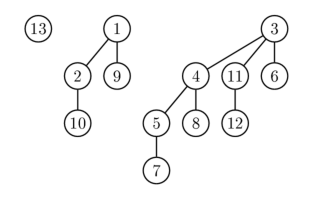
Beispiel eines Binomialheaps mit den Schlüsselelementen 1, 2, ..., 13. Der Heap besteht aus 3 Binomialbäumen der Ordnung 0, 2 und 3.
Implementierung von Operationen
Am interessantesten ist vielleicht die Operation zum Zusammenführen von zwei Heaps, die in den meisten anderen Operationen wiederverwendet wird. Die Stammlisten der beiden Heaps werden gleichzeitig durchsucht, ebenso wie die Zusammenführungssortierung . Wenn nur einer der beiden Heaps einen Baum der Ordnung j enthält , wird er dem zusammengeführten Heap hinzugefügt. Wenn die beiden Haufen einen Baum der Ordnung j enthalten , werden die beiden Bäume unter Berücksichtigung der Haufenstruktur zu einem Baum der Ordnung j + 1 zusammengeführt (die größere der beiden Wurzeln wird eine Tochter der kleineren). Beachten Sie, dass wir diesen Baum möglicherweise mit einem Baum der Ordnung j + 1 zusammenführen müssen , der in einem der beiden Anfangshaufen vorhanden ist. Während des Algorithmus untersuchen wir höchstens 3 Bäume jeder Ordnung (zwei aus den zwei zusammengeführten Haufen und einer aus zwei kleineren Bäumen). Die maximale Ordnung eines Baumes ist jedoch ln n und daher ist die Komplexität der Fusion in O (ln n) .
Um ein neues Element in einen Heap einzufügen, erstellen wir einfach einen neuen Heap, der nur dieses Element enthält, das wir dann mit dem ursprünglichen Heap zusammenführen, und dies in O (ln n) .
Um das kleinste Element des Haufens zu finden, reicht es aus, das Minimum unter den Wurzeln der Binomialbäume zu finden (bei der maximalen Anzahl von ln n ), was wiederum in O (ln n) erfolgt .
Um das kleinste Element aus dem Heap zu entfernen, suchen wir zuerst dieses Element, um es aus seinem Binomialbaum zu entfernen. Wir erhalten dann eine Liste der Teilbäume, die wir in einen anderen Binomialheap umwandeln und dann mit dem vorherigen Heap zusammenführen.
Wenn man den Schlüssel eines Gegenstands senkt , kann er kleiner als der des Vaters werden und die Heap-Reihenfolge des Baumes verletzen. In diesem Fall tauschen wir das Element mit seinem Vater aus, sogar mit seinem Großvater usw., bis der Baum wieder auf einem Haufen bestellt ist. Jeder Binomialbaum mit der maximalen Größe ln n ist die Operation in O (ln n) .
Um ein Element zu löschen , geben wir es schließlich für Schlüssel minus unendlich (kleiner als alle anderen Schlüssel ...) und löschen dann das kleinste Element aus dem Heap, dh sich selbst.
Verweise
- (fr) Dieser Artikel stammt teilweise oder vollständig aus dem englischen Wikipedia- Artikel " Binomial Heap " ( siehe Autorenliste ) .
- (en) Thomas H. Cormen , Charles E. Leiserson und Ronald L. Rivest , Einführung in Algorithmen , MIT Press ,1990[ Detail der Ausgabe ]
- (en) J. Vuillemin, " Eine Datenstruktur zum Manipulieren von Prioritätswarteschlangen ", in Communications of the ACM 21 (1978), 309-314.
