Logistiksuite

In der Mathematik ist eine logistische Sequenz eine einfache Sequenz , deren Wiederholung jedoch nicht linear ist. Seine Wiederholungsbeziehung ist

xnicht+1=μxnicht((1- -xnicht), x0∈[0;;1]].{\ displaystyle x_ {n + 1} = \ mu x_ {n} (1-x_ {n}), ~ x_ {0} \ in [0; 1].}

Abhängig vom Wert des Parameters μ (in [0; 4], um sicherzustellen, dass x in [0; 1] bleibt) wird eine konvergente Sequenz, eine Oszillationssequenz oder eine chaotische Sequenz erzeugt .

Oft als Beispiel für die genannte Verhalten Komplexität , die aus einer einfachen nicht - linearen Beziehung entstehen kann, wurde diese Fortsetzung von Biologen popularisiert Robert May in 1976 . Eine Anwendung der Logistiksuite ist die Modellierung der Größe einer biologischen Population über Generationen hinweg.

Es ist die zeitdiskrete Lösung des Verhulst-Modells . Der Begriff „Logistik“ stammt aus der Arbeit von Pierre François Verhulst, der die Logistikkurve als zeitkontinuierliche Lösung seines Modells bezeichnet. Er schrieb 1845 in seiner Arbeit, die sich diesem Phänomen widmete: "Wir werden dieser Kurve den Begriff Logistik geben" . Der Autor erklärt seine Wahl nicht, aber „Logistik“ hat dieselbe Wurzel wie Logarithmus und logistikos bedeutet auf Griechisch „Berechnung“.

Verhalten nach μ

Im logistischen Modell werden wir berücksichtigen, dass die hier angegebene Variable x n das Verhältnis der Population einer Art zur maximalen Population dieser Art bezeichnet (es ist eine Zahl zwischen 0 und 1). Durch Variieren des Parameters μ werden verschiedene Verhaltensweisen beobachtet:

Fall 0 ≤ µ ≤ 1 die Bevölkerung ist ausgelöscht.

Schließlich wird die Art unabhängig von der Ausgangspopulation sterben. Dh . lim+∞xnicht=0{\ displaystyle \ lim _ {+ \ infty} x_ {n} = 0}

Fall 1 ≤ µ ≤ 3 Die Bevölkerungszahl stabilisiert sich.

• Wenn 1 ≤ µ ≤ 2 ist , stabilisiert sich die Population unabhängig von der ursprünglichen Population um den Wert . Mit anderen Worten .μ- -1μ{\ displaystyle {\ frac {\ mu -1} {\ mu}}}lim+∞xnicht=μ- -1μ{\ displaystyle \ lim _ {+ \ infty} x_ {n} = {\ frac {\ mu -1} {\ mu}}}
• Wenn 2 ≤ µ ≤ 3 ist , stabilisiert es sich auch nach einiger Zeit des Schwingens. Die Konvergenzgeschwindigkeit ist linear, mit Ausnahme von µ = 3, wo sie sehr langsam ist.μ- -1μ{\ displaystyle {\ frac {\ mu -1} {\ mu}}}

Fall 3 ≤ µ ≤ 3,57 Die Größe der Bevölkerung schwankt zwischen 2, 4, 8… Werten (Potenz von 2).

• Wenn 3 <µ ≤ 1 + √6 (ungefähr 3,45) ist, schwankt es zwischen zwei Werten, abhängig von µ, aber nicht von der Anfangspopulation.
• Wenn 3,45 <µ <3,54 (ungefähr) ist, schwankt es zwischen vier Werten, wiederum abhängig von µ, aber nicht von der Anfangspopulation.
• Wenn µ etwas größer als 3,54 ist, schwankt die Grundgesamtheit zwischen acht Werten, dann 16, 32 usw. Das Werteintervall von µ , das zu der gleichen Anzahl von Schwingungen führt, nimmt schnell ab. Das Verhältnis zwischen zwei dieser aufeinanderfolgenden Intervalle nähert sich jedes Mal, wenn die Feigenbaumsche Konstante δ = 4,669…. Keines dieser Verhaltensweisen hängt von der ursprünglichen Grundgesamtheit ab.

Fall 3,57 ≤ µ Die Bevölkerungszahl ist mit einigen Ausnahmen chaotisch .

• Um µ = 3,57 setzt Chaos ein. Es ist noch keine Schwingung sichtbar und geringfügige Abweichungen in der Anfangspopulation führen zu radikal unterschiedlichen Ergebnissen.
• Die meisten Werte über 3,57 weisen einen chaotischen Charakter auf, aber es gibt einige isolierte Werte von µ mit einem Verhalten, das nicht der Fall ist. Zum Beispiel zeigt ab 1 + √8 (ungefähr 3,82) ein kleines Werteintervall von µ eine Schwingung zwischen drei Werten und für µ etwas größer zwischen sechs Werten, dann zwölf und so weiter. Andere Intervalle bieten Schwingungen zwischen 5 Werten usw. Alle Schwingungsperioden sind wieder vorhanden, wiederum unabhängig von der Grundgesamtheit.
• Jenseits von µ = 4 verlässt das Verhältnis der Population der Art zur Maximalpopulation das Intervall [0,1] und divergiert fast für alle Anfangswerte.

Die oben beschriebenen Schwingungsperioden erfüllen die folgende Regel. Betrachten Sie die Charkovski-Ordnung, die für streng positive ganze Zahlen definiert ist, wie folgt:

3◃5◃7◃...◃2×3◃2×5◃2×7◃...◃2nicht×3◃2nicht×5◃2nicht×7◃...{\ displaystyle 3 \; \ triangleleft \; 5 \; \ triangleleft \; 7 \; \ triangleleft \; \ ldots \; \ triangleleft \; 2 \ times 3 \; \ triangleleft \; 2 \ times 5 \; \ triangleleft \; 2 \ mal 7 \; \ triangleleft \; \ ldots \; \ triangleleft \; 2 ^ {n} \ times 3 \; \ triangleleft \; 2 ^ {n} \ times 5 \; \ triangleleft \; 2 ^ {n} \ times 7 \; \ triangleleft \; \ ldots} ◃2nicht+1×3◃2nicht+1×5◃...◃2nicht◃2nicht- -1◃...◃22◃2◃1{\ displaystyle \; \ triangleleft \; 2 ^ {n + 1} \ times 3 \; \ triangleleft \; 2 ^ {n + 1} \ times 5 \; \ triangleleft \; \ ldots \; \ triangleleft \; 2 ^ {n} \; \ triangleleft \; 2 ^ {n-1} \; \ triangleleft \; \ ldots \; \ triangleleft \; 2 ^ {2} \; \ triangleleft \; 2 \; \ triangleleft \; 1 }} Mit anderen Worten, wir platzieren zuerst die ungeraden ab 3 in aufsteigender Reihenfolge, dann die ungeraden multipliziert mit 2, dann mit 4 usw. und wir enden mit den Potenzen von 2 in absteigender Reihenfolge. Wenn ein Wert des Parameters µ einer Schwingungsperiode n entspricht , entsprechen alle Ganzzahlen, die in Charkovskis Reihenfolge auf n folgen, Schwingungsperioden, die bereits für Werte des Parameters kleiner als µ aufgetreten sind . Da also µ = 3,82 einer Periode 3 entspricht, sind bereits alle möglichen Schwingungsperioden für Werte von µ zwischen 0 und 3,82 aufgetreten .

Ein Bifurkationsdiagramm  (in) , mit dem die verschiedenen Fälle grafisch zusammengefasst werden:

Bemerkungen

Einige einfache Überlegungen und einige Grafiken geben teilweise Aufschluss über die obigen Ergebnisse.

Grafik

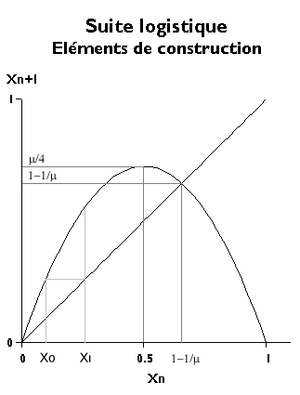
Die Entwicklung der logistischen Sequenz kann in der Ebene dargestellt werden ( x n , x n + 1 ).

Die Grundgleichung stellt eine Parabel dar, die durch die Punkte der Abszisse 0 und 1 auf der horizontalen Achse verläuft. Damit die Werte von x n + 1 nicht negativ werden, muss nur der zwischen diesen beiden Punkten enthaltene Bogen beibehalten werden. dies ergibt für x n = 1 ⁄ 2 ein Maximum des Wertes μ ⁄ 4 . Dieser Wert muss ebenfalls zwischen 0 und 1 liegen, daher μ <4.

Wenn die Sequenz konvergiert, erfüllt ihre Grenze die Gleichung lim x n + 1 = lim x n . Diese mit x bezeichnete mögliche Grenze ist die Lösung der quadratischen Gleichung

x=μx((1- -x){\ displaystyle x = \ mu x (1-x)}

und kann daher den einen oder anderen der Werte annehmen

x=0,x=1- -1/.μ{\ displaystyle x = 0, x = {1- {1 / \ mu}}}

Um das Verhalten der Sequenz zu beschreiben, ist es notwendig, von einer Abszisse x 0 auszugehen , auf der Parabel den Wert x 1 zu bestimmen, der dann in eine neue Abszisse umgewandelt wird, die durch die Winkelhalbierende x n + 1 = x n verläuft, und diese beiden zu wiederholen Operationen.

Konvergenzbereiche

Für bestimmte Werte des Parameters μ verhält sich die Sequenz wie eine klassische Sequenz und konvergiert gegen eine der beiden möglichen Grenzen. Die Grundgleichung kann in der Form umgeschrieben werden

xnicht+1xnicht=μ((1- -xnicht){\ displaystyle {x_ {n + 1} \ over x_ {n}} = \ mu (1-x_ {n})}

Wenn , ist die Sequenz durch eine geometrische Sequenz begrenzt, die gegen 0 tendiert. 0≤μ≤1{\ displaystyle 0 \ leq \ mu \ leq 1}

Um das Verhalten in Bezug auf die zweite mögliche Grenze zu sehen, reicht es aus, die Änderung der Variablen x n = u n + 1 - 1 / μ durchzuführen . Die Formel lautet:

unicht+1+1- -1/.μunicht+1- -1/.μ=1- -μunicht{\ displaystyle {{u_ {n + 1} + 1-1 / \ mu} \ over {u_ {n} + 1-1 / \ mu}} = 1- \ mu u_ {n}}

In diesem Fall erfordert die Konvergenzbedingung, dass das zweite Element zwischen -1 und + 1 liegt : . 1≤μ≤3{\ displaystyle 1 \ leq \ mu \ leq 3}

Wir überprüfen, ob, wenn u n nahe der Grenze 1 - 1 / μ liegt, 1 - μ u n nahe 2 - μ liegt und u n zu seiner Grenze tendiert, indem wir die Werte erhöhen, wenn μ kleiner als 2 ist, um Wechselwerte, wenn sie größer als 2 sind.

Gabelungen

Im vorherigen Absatz ermöglichte die Wiederholungsformel der Form x n + 1 = f ( x n ), die ersten Attraktoren zu erhalten, indem nach einer möglichen Grenze gesucht wurde, die der Gleichung x = f ( x ) entspricht.

Wenn μ größer als 3 wird, müssen wir eine Lösung für die Gleichung x = f ( f ( x )) finden. Dies führt zu einer Gleichung vierten Grades, bei der die Wurzeln natürlich bereits bekannt sind - aber sie sind keine Attraktoren mehr - und das Paar neuer Wurzeln. 0,1- -1μ{\ displaystyle 0,1 - {\ frac {1} {\ mu}}}

12((1+μμ±1μμ2- -2μ- -3){\ displaystyle {1 \ over 2} \ left ({1+ \ mu \ over \ mu} \ pm {1 \ over \ mu} {\ sqrt {\ mu ^ {2} -2 \ mu -3}} \ Recht)}

Es gibt keine Konvergenz mehr: Es erscheint ein Grenzzyklus. Das Ergebnis der Iteration wechselt abwechselnd von einer der letzten beiden Wurzeln zur anderen: u n + 1 = u n-1, während u n + 2 = u n . Für μ = 3,4 erscheinen die aufeinanderfolgenden Näherungswerte 0,84, 0,45, 0,84, 0,45, 0,84 ....

Jenseits der Stabilitätsgrenze dieses Zyklus, √6 + 1, treten zwei neue Verzweigungen auf, die von den Lösungen von x = f (f (f (f (x))) abhängen. Für μ = 3,47 liegen die aufeinanderfolgenden Werte in der Größenordnung von 0,47, 0,86, 0,40, 0,84, 0,47 ...

Chaos

Von Bifurkation zu Bifurkation werden die Entwicklungen immer komplexer. Der Prozess führt für ungefähr μ> 3,57 zu Systemen, die im Allgemeinen keine sichtbaren Attraktoren mehr aufweisen. Die Grafiken stellen dann eine „chaotische“ Entwicklung im üblichen Sinne des Wortes dar.

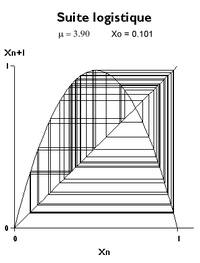
In der Sprache der Mathematiker bedeutet das Wort Chaos jedoch eine starke Sensibilität für die Anfangsbedingungen. Die beiden Graphen entsprechend μ = 3,9 mit den Anfangswerten u 0 0,100 und 0,101 zeigen, dass sich die Trajektorien voneinander entfernen, bis sie sich schnell unterscheiden. In einem konkreten Problem sind die Anfangsbedingungen nie genau bekannt: Nach einer bestimmten Zeit ist ein chaotisches Phänomen unvorhersehbar geworden, obwohl das Gesetz, das es definiert, vollkommen deterministisch ist.

Anhänge

Literaturverzeichnis

• Alain Hillion , Die mathematischen Theorien der Bevölkerung , Paris, Presses universitaire de France , Slg.  "  Was weiß ich  "1986127  p. Nr. 2258 ( ISBN  2-13-039193-1 )
• Nicolas Bacaër , Geschichte der Mathematik und der Bevölkerung , Paris, Éditions Cassini, Slg.  "Salz und Eisen",2008212  p. ( ISBN  978-2-84225-101-7 , Hinweis BnF n o  FRBNF42035729 ) , "Verhulst und die logistische Gleichung"

Zum Thema passende Artikel

• Dynamisches System
• Chaostheorie
• Ergodentheorie
• Lyapunov-Fraktal
• Feedback , Selbstregulierung

Externe Links

• (en) Elmer G. Wiens, Die Logistikkarte und das Chaos
• [PDF] Daniel Perrin, Die Logistiksuite und das Chaos
• (fr) Interaktive digitale Erfahrung des Bifurkationsdiagramms der Logistikanwendung http://experiences.math.cnrs.fr

Anmerkungen und Referenzen

1. (in) RM May , "  Einfache mathematische Modelle mit sehr komplizierter Dynamik  " , Nature , vol.  261, n o  55601976, p.  459–467 ( DOI  10.1038 / 261459a0 )
2. (in) Warum nicht autokatalytische und Gefechtskopf-Logistikkurve?