Quadric

In der Mathematik ist eine quadratische oder quadratische Fläche eine Fläche, die eine kartesische Polynomgleichung vom Grad 2 mit drei Variablen (allgemein bekannt als x , y und z ) der Form erfüllt

BEIMx2+B.y2+VSz2+2D.yz+2E.xz+2F.xy+Gx+H.y+ichz+J.=0{\ displaystyle Axe ^ {2} + By ^ {2} + Cz ^ {2} + 2Dyz + 2Exz + 2Fxy + Gx + Hy + Iz + J = 0}.

Diese Oberflächen werden durch eine reduzierte Gleichung in einem orthonormalen Rahmen klassifiziert, der in der euklidischen Geometrie angepasst ist , und in neun nicht entarteten Klassen bis zur linearen Transformation in der affinen Geometrie . Sie können auch im Rahmen der projektiven Geometrie untersucht werden , was die Ergebnisse vollständig vereinfacht und vereinheitlicht.

Ihre ebenen Abschnitte sind Kegel .

Die Definition ist in höherer Dimension mit dem Begriff der verallgemeinerten affiner quadric , eine Hyperfläche als der charakterisierten Ort der Annullierung  (in) ein Polynom vom Grad 2, sogar auf einem anderen Körper von Koeffizienten als das der reellen Zahlen .

Einstufung

Präsentation der Hauptquadriken

Die nicht entarteten Quadriken werden nachstehend anhand ihrer reduzierten Gleichungen in einem geeigneten orthonormalen Rahmen beschrieben.

Das Ellipsoid	x2beim2+y2b2+z2vs.2- -1=0{\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} + {\ frac {z ^ {2} } {c ^ {2}}} - 1 = 0 \,} ,
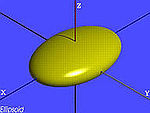
Das einblättrige Hyperboloid (H1)	x2beim2+y2b2- -z2vs.2- -1=0{\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} - {\ frac {z ^ {2} } {c ^ {2}}} - 1 = 0 \,} ,
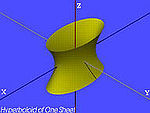
Das Zwei-Blatt-Hyperboloid (H2)	x2beim2+y2b2- -z2vs.2+1=0{\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} - {\ frac {z ^ {2} } {c ^ {2}}} + 1 = 0 \,} ,
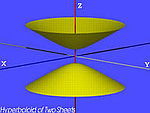
Das elliptische Paraboloid (PE)	x2beim2+y2b2=z{\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} = z \,} ,
Das hyperbolische Paraboloid (PH)	x2beim2- -y2b2=z{\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} - {\ frac {y ^ {2}} {b ^ {2}}} = z \,} ,
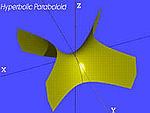
Der elliptische Grundkegel	x2beim2+y2b2- -z2vs.2=0{\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} - {\ frac {z ^ {2} } {c ^ {2}}} = 0 \,} ,
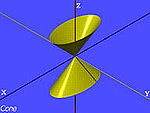
Der elliptische Zylinder	x2beim2+y2b2- -1=0{\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} - 1 = 0 \,} ,
Der hyperbolische Zylinder	x2beim2- -y2b2- -1=0{\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} - {\ frac {y ^ {2}} {b ^ {2}}} - 1 = 0 \,} ,
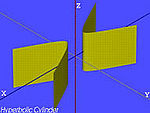
Der Parabolzylinder	x2=2py{\ displaystyle \ displaystyle {x ^ {2} = 2py}} .

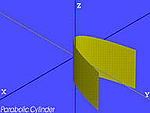
Allgemeine Einteilung

Die Oberflächengleichung kann geschrieben werden:

Q.((x,y,z)+Gx+H.y+ichz+J.=0 {\ Anzeigestil Q (x, y, z) + Gx + Hy + Iz + J = 0 ~}

wobei Q die quadratische Form bezeichnet

Q.((x,y,z)=BEIMx2+B.y2+VSz2+2D.yz+2E.xz+2F.xy {\ displaystyle Q (x, y, z) = Ax ^ {2} + By ^ {2} + Cz ^ {2} + 2Dyz + 2Exz + 2Fxy ~}

Matrix:

M.Q.=((BEIMF.E.F.B.D.E.D.VS){\ displaystyle M_ {Q} = {\ begin {pmatrix} A & F & E \\ F & B & D \\ E & D & C \ end {pmatrix}}}

deren Eigenwerte alle reell sind, da diese Matrix reell symmetrisch ist .

Die Signatur der quadratischen Form ist das Paar (p, q), wobei p die Anzahl der streng positiven Eigenwerte von Q und q die Anzahl der streng negativen Eigenwerte ist. Der Rang von Q ist dann p + q . Per Definition eines Quadrats kann der Rang von Q nicht Null sein. Die Tatsache, dass die Signatur einer quadratischen Form nicht von der Wahl der gewählten Basis abhängt, zeigt das Trägheitsgesetz von Sylvester .

Wenn der Rang gleich 3 ist, lässt die Quadrik ein Symmetriezentrum zu.

Rang	Unterschrift	Nicht entartetes Quadrat	Entartete Quadrik
3	(3,0) oder (0,3)	Ellipsoid	∅{\ displaystyle \ varnothing} oder Punkt
	(2,1) oder (1,2)	Hyperboloid mit 1 oder 2 Schichten oder Kegel
2	(2,0) oder (0,2)	elliptisches Paraboloid oder elliptischer Zylinder	∅{\ displaystyle \ varnothing} oder richtig
	(1.1)	hyperbolisches Paraboloid oder hyperbolischer Zylinder	Treffen zweier Pläne
1	(1,0) oder (0,1)	Parabolzylinder	∅{\ displaystyle \ varnothing} oder Plan oder Kombination von zwei Plänen

Demonstration

Zur Vereinfachung werden die Koordinaten nach den folgenden Änderungen der orthonormalen Referenzmarken immer mit x , y und z notiert .

Die Matrix der quadratischen Form, sauber Nennwerte , , wird unter Verwendung einer orthogonale Transformations - Matrix auf Diagonal. In einem neuen orthonormalen Koordinatensystem wird die Gleichung der Oberfläche geschrieben α {\ displaystyle \ alpha ~}β {\ displaystyle \ beta ~}γ {\ displaystyle \ gamma ~}

αx2+βy2+γz2+px+qy+rz=k {\ displaystyle \ alpha x ^ {2} + \ beta y ^ {2} + \ gamma z ^ {2} + px + qy + rz = k ~}.

Wenn beispielsweise einer der Eigenwerte ungleich Null ist, kann die entsprechende Koordinate zentriert werden: α {\ displaystyle \ alpha ~}

αx2+px=α((((x+p2α)2- -((p2α)2){\ displaystyle \ alpha x ^ {2} + px = \ alpha ((x + {\ frac {p} {2 \ alpha}}) ^ {2} - ({\ frac {p} {2 \ alpha}} ) ^ {2})}

Dies läuft darauf hinaus, eine Übersetzung oder eine Änderung des Ursprungs des Referenzrahmens durchzuführen.

• Wenn der Rang gleich drei ist, sind die drei Eigenwerte nicht Null; In einem neuen orthonormalen Koordinatensystem lautet die Gleichung:

αx2+βy2+γz2=K. {\ displaystyle \ alpha x ^ {2} + \ beta y ^ {2} + \ gamma z ^ {2} = K ~}.

• • Wenn die Signatur (3.0) oder (0.3) wert ist, haben die drei Eigenwerte das gleiche Vorzeichen. Wenn K Null ist, ist es ein Punkt; Andernfalls ist es ein Ellipsoid, wenn K das Vorzeichen der Eigenwerte und ansonsten der leeren Menge hat.
  • Wenn die Signatur (2,1) oder (1,2) wert ist, haben zwei Eigenwerte das gleiche Vorzeichen, was wir hier als Mehrheit bezeichnen werden. wenn K Null ist, ist es ein Kegel; Andernfalls handelt es sich um ein einblättriges Hyperboloid, wenn K das Mehrheitszeichen hat, und andernfalls um ein zweiblättriges Hyperboloid.

• Wenn der Rang gleich zwei ist, ist einer der Eigenwerte Null und zum Beispiel nur einer ; In einem neuen orthonormalen Koordinatensystem lautet die Gleichung:γ {\ displaystyle \ gamma ~}

αx2+βy2+rz=K. {\ displaystyle \ alpha x ^ {2} + \ beta y ^ {2} + rz = K ~}.

• • Wenn r nicht Null ist, erhalten wir ein elliptisches Paraboloid, wenn die beiden Nicht-Null-Eigenwerte das gleiche Vorzeichen haben, und ansonsten ein hyperbolisches Paraboloid, weil die Gleichung geschrieben ist:

αx2+βy2=- -r((z- -K.r{\ displaystyle \ alpha x ^ {2} + \ beta y ^ {2} = - r (z - {\ frac {K} {r}}}).

• • Wenn r Null ist und wenn K Null ist, ist es die Vereinigung zweier Ebenen, wenn die Nicht-Null-Eigenwerte ein entgegengesetztes Vorzeichen haben, und ansonsten eine gerade Linie.
  • Wenn r Null ist und K nicht Null ist, ist es ein hyperbolischer Zylinder, wenn die Nicht-Null-Eigenwerte ein entgegengesetztes Vorzeichen haben, und wenn nicht, ein elliptischer Zylinder, wenn K das Vorzeichen der Nicht-Null-Eigenwerte ist, und Sonst ist der Satz leer.

• Wenn der Rang gleich eins ist, ist beispielsweise nur ein Eigenwert ungleich Null ; In einem neuen orthonormalen Koordinatensystem lautet die Gleichung:β {\ displaystyle \ beta ~}

βy2+px+qy=K.  {\ displaystyle \ beta y ^ {2} + px + qy = K ~~},

dann nach einer letzten Änderung des orthonormalen Koordinatensystems

βy2+P.x=L.  {\ displaystyle \ beta y ^ {2} + Px = L ~~}.

Wenn P Null ist, erhalten wir eine Ebene, wenn L Null ist, und die Vereinigung zweier Ebenen oder der leeren Menge, je nachdem, ob L ein Vorzeichen von ist oder nicht. Ansonsten handelt es sich um einen Parabolzylinder. β{\ displaystyle \ beta}

Klassifizierung in affine Geometrie

Klassifizierung in projektive Geometrie

Quadrisch in jeder Dimension

Allgemeiner gesagt ist in einem Raum der Dimension D, wenn die Koordinaten des Raums sind , die allgemeine Quadrik eine Hyperfläche, die durch die algebraische Gleichung definiert ist: {x1,x2,...,xD.}}{\ displaystyle \ {x_ {1}, x_ {2}, \ dots, x_ {D} \}}

∑ich,j=1D.Q.ich,jxichxj+∑ich=1D.P.ichxich+R.=0{\ displaystyle \ sum _ {i, j = 1} ^ {D} Q_ {i, j} x_ {i} x_ {j} + \ sum _ {i = 1} ^ {D} P_ {i} x_ { i} + R = 0}

für eine bestimmte Wahl von Q, P und R.

Die normalisierte Gleichung für ein nicht entartetes Quadrat, das am Ursprung zentriert ist, hat folgende Form:

∑ich=1D.±xich2beimich2=1{\ displaystyle \ sum _ {i = 1} ^ {D} \ pm {x_ {i} ^ {2} \ über a_ {i} ^ {2}} = 1}

Anwendungen

In der Bildmodellierung

Für eine Gleichungsoberfläche liefert die Taylor-Young- Formel eine lokale Annäherung der Oberfläche durch das Gleichungsquadrat: z=f((x,y) {\ displaystyle z = f (x, y) ~}

p((x- -beim)+q((y- -b)+12[r((x- -beim)2+2s((x- -beim)((y- -b)+t((y- -b)2]]{\ Anzeigestil p (xa) + q (yb) + {\ frac {1} {2}} [r (xa) ^ {2} + 2s (xa) (yb) + t (yb) ^ {2}] }}

mit den sogenannten Monge- Notationen p=∂f∂x((beim,b),q=∂f∂y((beim,b),r=∂2f∂x2((beim,b),t=∂2f∂y2((beim,b),s=∂2f∂x∂y((beim,b).{\ displaystyle p = {\ frac {\ partielles f} {\ partielles x}} (a, b), q = {\ frac {\ partielles f} {\ partielles y}} (a, b), r = { \ frac {\ partiell ^ {2} f} {\ partiell x ^ {2}}} (a, b), t = {\ frac {\ partiell ^ {2} f} {\ partiell y ^ {2}} } (a, b), s = {\ frac {\ partiell ^ {2} f} {\ partiell x \ partiell y}} (a, b).}

Diese lokale Näherung wird bei der Bildmodellierung verwendet und liefert dort interessante Ergebnisse.

Anmerkungen und Referenzen

1. André Warusfel , „Quadriques“ , im Wörterbuch der Mathematik, Algebra, Analyse, Geometrie , Encyclopædia Universalis und Albin Michel,1997.
2. Weder leer noch auf einen Punkt, eine Linie, eine Ebene oder die Vereinigung zweier Ebenen reduziert.
3. Sylvie Philipp, Strukturmodellierung von Texturen. Extraktion des Primärkorns und seiner Platzierungsregel im zwölften Kollock Gretsi , Juan-les-Pins, 1988, Lire en ligne , p.  590 .
4. Alaa Mustafa, Beitrag zur Untersuchung diskreter Krümmungen und ihrer Anwendungen , 2008 [Dissertation].

Siehe auch

• Konisch

<img src="https://fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1x1" alt="" title="" width="1" height="1" style="border: none; position: absolute;">